Soal dan Pembahasan Matematika IPA SBMPTN 2018 Kode 449
Assalamu'alaikum semua :)
Semoga teman-teman sedang dalam keadaan sehat dan happy ya! Pada kesempatan kali ini saya akan share pembahasan Matematika IPA SBMPTN 2018 Kode 449. Perhatikan kembali, apabila ada kesalahan silahkan tulis di kolom komentar. Enjoy!
^^
Matematika IPA SBMPTN 2018 Kode 449 Nomor 1
Jika periode fungsi f(x) = 2cos(ax) + a adalah \(\frac{\pi}{3}\), maka nilai minimum fungsi f adalah ...
a. 1 b. 2 c. 4 d. 6 e. 8
Pembahasan:
Misalkan \(f(x)=a\sin(bx)+c\) maka diperoleh:
- Periode \(=\frac{360}{b}\)
- Nilai maksimum \(=a+c\)
- Nilai minimum \(=-a+c\)
Diketahui pada soal \(f(x) = 2\cos(ax) + a\) sehingga
- P \(=\frac{360}{a}=60\Leftrightarrow a=6 \)
- Min \(= -2+6=4\) (C)
Diketahui gradien garis yang melalui titik O(0,0) dan P(a,b) adalah -3. Jika P dicerminkan terhadap sumbu y kemudian digeser 5 satuan ke atas dan 2 satuan ke kanan, maka gradien garis yang melalui P' dan O(0,0) adalah 2. Titik P adalah ...
a. (-2,6) b. (-1,3) c. (1,-3) d. (2,-6) e. (3,-9)
Pembahasan:
Gradien yang melalui titik pusat \(O(0,0)\) dan titik \(P(x,y)\) adalah \(m=\frac{y}{x}\), maka diperoleh:
\(O(0,0), P(a,b)\to m_1=-3\)
\(\Leftrightarrow m_1=\frac{b}{a}=-3\)
\(b=-3a\)
\(P(a,b)\xrightarrow[]{\textrm{refleksi sb-y}} (-a,b)\xrightarrow[]{\textrm{translasi (2,5)}} (-a+2,b+5)\)
\(\Leftrightarrow m_2=2\)
\(\frac{b+5}{-a+2}=2\)
\(\frac{-3a+5}{-a+2}=2\)
\(-3a+5=-2a+4\)
\(a=1\)
\(b=-3(1)=-3\)
Maka \(P(1,-3)\) (C)
Matematika IPA SBMPTN 2018 Kode 449 Nomor 3
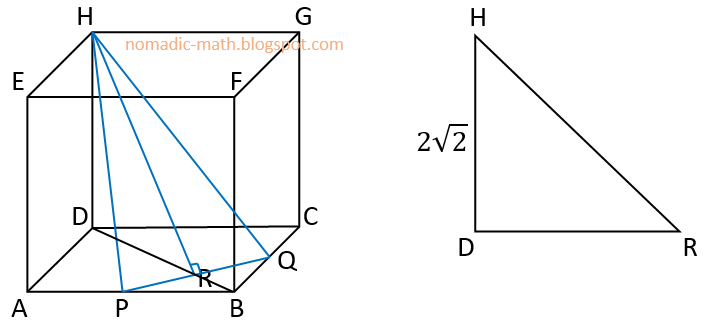
Diketahui kubus ABCD.EFGH dengan panjang rusuk \(2\sqrt2\) cm. Jika titik P di tengah-tengah AB dan titik Q di tengah-tengah BC, maka jarak antara titik H dengan PQ adalah ... cm
a. \(\sqrt{15}\) b. \(4\) c. \(\sqrt{17}\) d. \(3\sqrt2\) e. \(\sqrt{19}\)
Pembahasan:
\(\displaystyle \lim_{x \to \infty }\frac{8}{\sqrt{x^2+2x}-\sqrt{x^2-6x}}=\) ...
a. 0 b. 1 c. 2 d. 4 e. 8
Pembahasan:
Ingat, untuk \(\displaystyle \lim_{x \to \infty } \) bentuk (\(\infty-\infty\)) maka:
\(\displaystyle \lim_{x \to \infty }\sqrt{ax^2+bx+c}-\sqrt{px^2+qx+r} =\begin{cases}+\infty \text{ untuk } a>p \\-\infty \text{ untuk } a<p \\\frac{b-q}{2\sqrt{a}} \text{ untuk } a=p \end{cases}\)
\(\displaystyle \lim_{x \to \infty }\frac{8}{\sqrt{x^2+2x}-\sqrt{x^2-6x}}\)
\(=\frac{\displaystyle \lim_{x \to \infty}8}{\displaystyle \lim_{x \to \infty}\sqrt{x^2+2x}-\sqrt{x^2-6x}}\)
\(=\frac{8}{\frac{2-(-6)}{2\sqrt1}}\)
\(=\frac{8}{\frac{8}{2}}\)
\(=2\) (C)
Matematika IPA SBMPTN 2018 Kode 449 Nomor 5
Misalkan a + 3, a - 1, 2 membentuk barisan geometri, maka jumlah 11 suku pertama yang mungkin adalah ...
a. 1 b. 2 c. 4 d. 6 e. 8
Pembahasan:
\(\text{rasio}\to\frac{a-1}{a+3}=\frac{2}{a-1}\)
\(2a+6=a^2-2a+1\)
\(a^2-4a-5=0\)
\((a-5)(a+1)=0\)
\(a=5\) U \(a=-1\)
\(a=5\to8,4,2,1,\frac{1}{2},...\to r=\frac{1}{2}\)
\(a=-1\to2,-2,2,-2,...\to r=-1\)
Perhatikan, di pilihan ganda jumlahnya berupa bilangan bulat sehingga jawaban yang mungkin adalah jika \(a=-1\), maka akan diperoleh \(S_{11}=2\)
\(S_{11}=\frac{a(1-r^n)}{1-r}=\frac{2(1-(-1)^{11})}{2}=2\) (B)
Matematika IPA SBMPTN 2018 Kode 449 Nomor 6
Daerah R dibatasi oleh \(y=ax^4,y=a,x=2\) dan garis sumbu x positif. Jika volume benda padat yang didapat dengan memutar R terhadap sumbu x adalah \(\frac{40}{9}\pi,\) maka a = ...
a. 5 b. 4 c. 3 d. 2 e. 1
Pembahasan:
Dengan batas \(y=ax^4,y=a,x=2, \text{sb-x positif}\) maka terbentuk ilustrasi sebagai berikut,
Karena batas atas dan bawahnya berbeda, maka kita perlu bagi menjadi dua daerah. Pertama, cari titik perpotongannya:
\(y=ax^4\)
\(a=ax^4\)
\(x^4=1\)
\(x=\pm1\) (pilih \(x=1\))
Kedua, hitung volumenya:
\(\pi\int_{0}^{1}(ax^4)^2dx+\int_{1}^{2}(a)^2dx=\frac{40}{9}\pi\)
\(\int_{0}^{1}(a^2x^8)dx+\int_{1}^{2}(a^2)dx=\frac{40}{9}\)
\(\left [\frac{a^2}{9}x^9 \right ]_{0}^{1}+\left [ a^2x \right ]_{1}^{2}=\frac{40}{9}\)
\(\frac{a^2}{9}-0+2a^2-a^2=\frac{40}{9}\)
\(\frac{a^2}{9}+a^2=\frac{40}{9}\to\) (ruas kiri kanan dikali 9)
\(a^2+9a^2=40\)
\(10a^2=40\)
\(a^2=4\)
\(a=\pm2\) (D)
Matematika IPA SBMPTN 2018 Kode 449 Nomor 7
Ari dan Ira merupakan anggota dari suatu kelompok yang terdiri dari 9 orang. Banyaknya cara membuat barisan, dengan syarat Ari dan Ira tidak berdampingan adalah ...
a. 7 \(\times\) 8!
b. 8 \(\times\) 8!
c. 5 \(\times\) 8!
d. 7 \(\times\) 7!
e. 6 \(\times\) 7!
Pembahasan:
Banyak cara membentuk barisan: \(=9!\)
Ari dan Ira berdampingan:
Maka Ari dan Ira tidak berdampingan adalah
\(=9!-8!\cdot 2!\)
\(=9\cdot8!-2\cdot8!\)
\(=8!(9-2)\)
\(=7\cdot8!\) (A)
Matematika IPA SBMPTN 2018 Kode 449 Nomor 8
Jika panjang jari-jari lingkaran \(x^2+y^2+Ax+2Ay+C=0\) dan \(x^2+y^2+Ax+3Ay+C=0\) berturut-turut adalah \(1\) dan \(\sqrt6,\) maka nilai dari C adalah ...
a. 1 b. 2 c. 3 d. 4 e. 5
Pembahasan:
\(x^2+y^2+Ax+2Ay+C=0\to r_1=1\)
\(r=\sqrt{(-\frac{1}{2}A)^2+(-\frac{1}{2}B)^2-C}\)
\(1=\sqrt{(-\frac{1}{2}A)^2+(-\frac{1}{2}\cdot2A)^2-C}\)
\(1=\frac{1}{4}A^2+A^2-C\)
\(1=\frac{5}{4}A^2-C... (1)\)
\(x^2+y^2+Ax+3Ay+C=0\to r_2=\sqrt{6}\)
\(\sqrt{6}=\sqrt{(-\frac{1}{2}A)^2+(-\frac{1}{2}\cdot3A)^2-C}\)
\(6=\frac{1}{4}A^2+\frac{9}{4}A^2-C\)
\(6=\frac{5}{2}A^2-C... (2)\)
Pers \((1)\) dikali \(2\), diperoleh \(2+2C=\frac{5}{2}A^2...(3)\)
Substitusi \((3)\) pada \((2)\) maka,
\(6=2+2C-C\)
\(C=4\) (D)
Sisa pembagian \(p(x)=x^3-ax^2-2bx-4a-4\) oleh \(x^2+1\) adalah \(-5a+2\). Jika \(p(x)\) dibagi \(x-1\) bersisa -17, maka 4ab = ...
a. -12 b. -9 c. -7 d. -6 e. -5
Pembahasan:
\(x-a\)
\(x^2+1/\overline{x^3-ax^2-2bx-4a-4}\)
\(x^3+x\) \(-\)
\(\overline{-ax^2-(2b+1)x-4a-4}\)
\(-ax^2-a\) \(-\)
\(\overline{-(2b+1)x-3a-4}\) \(=-5a+2\)
Diperoleh \(-2b-1=0\) dan \(-3a-4=-5a+2\)
\(-2b-1=0\)
\(-2b=1\)
\(b=-\frac{1}{2}\)
\(-3a-4=-5a+2\)
\(2a=6\)
\(a=3\)
Jadi, \(4ab=4\cdot \left (- \frac{1}{2} \right )\cdot 3=-6\) (D)
Matematika IPA SBMPTN 2018 Kode 449 Nomor 10
Jika garis singgung kurva \(y=-2x^3\) di titik P(a,b) memotong sumbu y di titik Q(0,4), maka a + b adalah ...
a. \(-1\) b. \(-\frac{1}{2}\) c. \(-\frac{1}{4}\) d. \(\frac{1}{4}\) e. \(1\)
Pembahasan:
\(y=-2x^3\) , \(P(a.b)\)
\(b=-2a^3\)
\(m=y'=-6x^2=-6a^2\)
PGS : \(y-y_1=m(x-x_1)\)
\(y-b=-6a^2(x-a)\)
memotong sb-y di \(Q(0,4)\)
\(4-b=-6a^2(0-a)\)
\(4-b=6a^3\)
lalu masukkan nilai \(b=-2a^3\)
\(4+2a^3=6a^3\)
\(4=4a^3\)
\(a=1\)
\(b=-2\cdot(1)^3\)
\(b=-2\)
Jadi, \(a+b=1+(-2)=-1\) (A)
Matematika IPA SBMPTN 2018 Kode 449 Nomor 11
Nilai \(\int_{\frac{1}{8}}^{\frac{1}{3}}\frac{3}{x^2}\sqrt{1+\frac{1}{x}}\) \(dx\) adalah ...
a. 19 b. 38 c. 57 d. 76 e. 95
Pembahasan:
misal: \(u=1+\frac{1}{x}=1+x^{-1}\)
\(x=\frac{1}{3}\rightarrow u=1+\frac{1}{1/3}=4\)
\(x=\frac{1}{8}\rightarrow u=1+\frac{1}{1/8}=9\)
\(du=-x^{-2}dx\)
\(du=-\frac{dx}{x^2}\)
\(dx=-x^{2}du\)
sehingga
\(=\int_{9}^{4}\frac{3}{x^2}\sqrt{u}\cdot -x^2du\)
\(=3\int_{9}^{4}u^{1/2}du\)
\(=-3\cdot\frac{1}{3/2}u^{3/2}|^4_{9}\)
\(=-2u\sqrt {u} |^4_{9}\)
\(=-2(4\sqrt{4}-9\sqrt{9})\)
\(=-2(8-27)=-2(-19)=38\) (B)
Diketahui \((a_n)\) dan \((b_n)\) adalah dua barisan aritmetika dengan \(a_1=5,a_2=8,b_1=8,\) dan \(b_2=7\). Jika \(A=\left\{ a_1,a_2,...,a_{100}\right\}\) dan \(B=\left\{ b_1,b_2,...,b_{100}\right\}\), maka banyaknya anggota \(A\cap B\) adalah ...
a. 20 b. 21 c. 22 d. 23 e. 24
Pembahasan:
\(u_n=a+(n-1)b\)
\(a_n\) dengan \(a_1=5, a_2=8\rightarrow b=3\)
\(a_n=5+(n-1)\cdot 3\)
\(=3n+2\)
\(A=\left \{ 5,8,11,14,17,20,23,...,302 \right \}\)
\(b_n\) dengan \(b_1=3, b_2=7\rightarrow b=4\)
\(b_n=3+(n-1)\cdot 4\)
\(=4n-1\)
\(B=\left \{ 3,7,11,15,19,23,...,399 \right \}\)
Perhatikan anggota \(A\) dan \(B\)
Maka,
\(A\cap B=\left \{ 11,23,... \right \} \rightarrow b=12\)
\(u_n=a+(n-1)b\)
\(=11+(n-1)\cdot 12\)
\(=12n-1\)
\(12n-1<302\)
\(12n<303\)
\(n<25,25\)
\(n=25\)
Jadi, \(n(A\cap B)=25\)
Matematika IPA SBMPTN 2018 Kode 449 Nomor 13
Himpunan semua bilangan real x pada selang [0,2π] yang memenuhi \(2-2\cos ^{2}x\leq \sqrt{3}\sin x\) berbentuk [a,b] ∪ [c,d]. Nilai a+b+c+d adalah ...
a. π b. 2π c. 3π d. 4π e. 5π
Pembahasan:
\(2-2\cos ^{2}x\leq \sqrt{3}\sin x\) \(,[0,2\pi]\)
\(2(1-\cos ^{2}x)\leq \sqrt{3}\sin x\)
\(2 \sin^{2}x\leq \sqrt{3}\sin x\)
\(2 \sin^{2}x - \sqrt{3}\sin x \leq0\)
\(\sin x(2\sin x -\sqrt{3})\leq 0\)
>> \(\sin x=0\)
\(x=0^{\circ}, x=180^{\circ}, x=360^{\circ}\)
>> \(2\sin x -\sqrt{3}=0\)
\(2\sin x =\sqrt{3}\)
\(\sin x=\frac{1}{2}\sqrt{3}\)
\(x=60^{\circ}, x=120^{\circ}\)
Ambil \(x=90^{\circ}\) maka \(1(2\cdot 1-\sqrt {3})=+\)
HP : {\(0\leq x\leq 60\) atau \(120\leq x\leq 180\)}
\([0,60] \cup [120,180] \Leftrightarrow [a,b] \cup [c,d]\)
Maka,
\(a+b+c+d=0+60+120+180\)
\(=360^{\circ}=2\pi\) (B)
Matematika IPA SBMPTN 2018 Kode 449 Nomor 14
Jika diketahui \(y=2^{3x^2+cx-1}\) dan \(y=4^{x^{2}-\frac{c}{2}}\) bersinggungan, maka c2+c = ...
a. 2 b. 6 c. 12 d. 20 e. 30
Pembahasan:
\(y=y\)
\(2^{3x^2+cx-1}=4^{x^{2}-\frac{c}{2}}\)
\(2^{3x^2+cx-1}=(2^2)^{x^{2}-\frac{c}{2}}\)
\(2^{3x^2+cx-1}=2^{2x^{2}-c}\)
Maka,
\(3x^2+cx-1=2x^{2}-c\)
\(x^2+cx-1+c=0\)
bersinggungan \(\rightarrow D=0\)
\(b^2-4ac=0\)
\(c^2-4\cdot 1\cdot (-1+c)=0\)
\(c^2-4c+4=0\)
\((c-2)^2=0\)
\(c-2=0\)
\(c=2\)
Diperoleh,
\(c^2+c=2^2+2=6\) (B)
Matematika IPA SBMPTN 2018 Kode 449 Nomor 15
Diketahui dua lingkaran x2+y2 = 2 dan x2+y2
= 4. Garis L1 menyinggung lingkaran pertama di titik (1,-1). Garis L2 menyinggung lingkaran kedua dan tegak lurus dengan garis L1. Titik potong garis L1 dan L2 adalah ...
a. \((1+\sqrt{2},\sqrt{2}-1)\)
b. \((1-\sqrt{2},\sqrt{2}-1)\)
c. \((1+\sqrt{2},\sqrt{2}+1)\)
d. \((1-\sqrt{2},\sqrt{2}-2)\)
e. \((1+\sqrt{2},\sqrt{2}+2)\)
Pembahasan:
\(x^2+y^2=2 \rightarrow\) titik singgung \((1,-1)\)
PGS. L1 : \(x_1x+y_1y=r^2\)
\(x-y=2 \rightarrow m_1=\frac{-a}{b}=\frac{-1}{-1}=1\)
\(L1\perp L2 \rightarrow m_2=-1\)
\(x^2+y^2=4\)
PGS. L2 : \(y=mx\pm r \sqrt {1+m^2}\)
\(y=-1x\pm 2\sqrt {1+1}\)
\(y=-x\pm 2\sqrt {2}\)
substitusikan \(x-y=2\)
\(x-(-x\pm 2\sqrt {2})=2\)
\(x+x\pm 2\sqrt {2}=2\)
\(2x=2\pm2\sqrt {2}\)
\(x=1\pm \sqrt {2}\)
\(x=1+\sqrt {2} \rightarrow y=-(1+\sqrt {2})+2\sqrt {2}\)
\(y=-1-\sqrt{2}+2\sqrt {2}\)
\(y=\sqrt{2}-1\)
Diperoleh \((1+\sqrt{2},\sqrt{2}-1)\) (A)
Untuk \(x=1-\sqrt {2}\) dicari dengan cara serupa.
***
Semoga bermanfaat ^^




Komentar
Posting Komentar